Determinants are mathematical scalar values associated with square matrices that can be used to solve linear equations efficiently.
However, it should be noted that determinants are calculated for a square matrix only.
Here, we will look into the different types of determinants that you can come across in mathematics.
If you ever need additional math help, there are really good derivative and matrix calculators available online that can show you the steps for any exercise.
How Can the Word “Determinant” be Defined?
There are several methods to define the determinant of a square matrix. One of the easiest ways to determine an impact size is to utilise the top row items and minors. Multiply each top-row element by its minor, then eliminate any product of that second-row element’s little and that first-row element.
Alternately add and delete the product of each component with its minor until all the components of the top row have been analysed.
Now, let’s look at the Characteristics, Properties or Types of Determinants, which will simplify its evaluation.
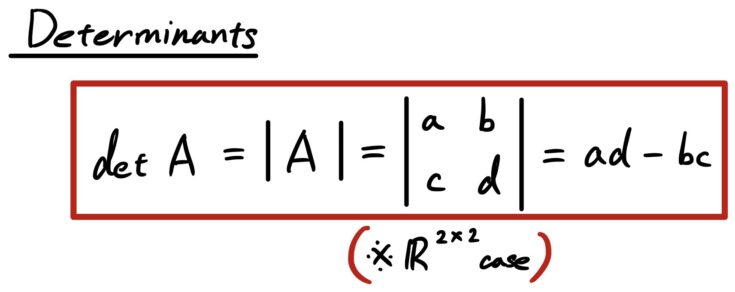
The Characteristics of Determinants
# A number may be obtained from a square matrix when using “determinant” in linear algebra contexts.
# For example, let’s assume we have a matrix with a determinant of P, which is det(P), |P|, or det P.
# We can acquire the same results with varied and more accessible input configurations because of determinants’ various properties, which are helpful (elements).
# According to the definition below, determinants are numerical values determined from a square matrix in Linear Algebra.
# For every square matrix, A = [aij] of order n, the determinant of the square matrix A is a number (real or complex) that may be correlated with A.
# The letter det A or the symbol |A| is used to represent it.
There are several characteristics of determinants that are quite beneficial since they allow us to produce the same outcomes with various and more straightforward arrangements of inputs (elements). By having a maximum number of zeros in a row or column, these determinant qualities make it easier to evaluate their value. Regardless of the order of the determinants, these features hold.
Reflection property, all-zero property, proportionality or repetition property, Switching property, multiple scalar property, sum property, invariance property, factor property, triangular property, and cofactor matrix property are the 10 most important qualities of determinants.
Features of Determinants
Transpose of a determinant (Reflection property)
It is the technique of swapping the rows and columns of a determinant matrix denoted by the phrase “transposition.” In the same process, the rows are changed into columns, then the columns are transformed back into rows, and so on. It is denoted by the symbol |AT| for any determinant |A|. The property |AT| = |A| says that the determinant does not change when transposes, i.e., |AT| = |A|.
Interchange of rows and columns (Switching Property)
The magnitude (that is, the sign) of the determinant changes when the order of any two rows or columns is changed, but the determinant value remains fixed.
At this point, the determinant value equals (-1) the number of deals executed.
Property with a value of zero
Because all related elements are equal, it is conceivable for two rows (or columns) of a single determinant to have the same value, but this is not the case.
Proof: If we swap the identical rows (or columns) of the determinant, the value of the determinant will stay the same as it was before. In the case of Property 2, however, it follows that the sign has been altered.
As a consequence, 0 = –0 or 0 = –0 is returned.
As an alternative, if we switch the first and second rows, the value of stays the same, but according to the previous property, it should be, and as a result, the equation equals
0 is the same as zero.
The Property of Proportionality (Repetition)
All items in one row (or column) are proportional (identical) to all of the components in another row (or column), and then the determinant is zero (or column).
Scalar Multiple Property
Scalar Multiple Properties are properties that have a large number of possible values. Suppose each determinant’s rows or columns are multiplied by the same scalar value, such as the constant k.
The result is that the fundamental factor is multiplied by the non-zero value of this constant. A real-world constant, maybe anything that exists in the actual world.
It is essential to notice that the determinant is multiplied with values from just one row rather than with components from the fundamental determinant, in this case. This trait is fundamental, and it can be shown rather easily via the use of expansion.
Sum Property
No restriction exists on the number of sub determinants that may be generated from a single main determinant, provided that they are all specified as a sum of two or more integers in the determinant’s row or column, as detailed in the next part of this document.
Property of Invariance
Any determinant’s value remains constant no matter how many rows (or columns) are involved in the operations. This is true for all determinants. In other words, the value of a determinant stays constant even if we multiply each element of one row (or column) by the equivalence of corresponding elements of the opposite row (or column) (or column).
Factor Property
As a result of the fact that by writing x=x, the determinant x becomes zero, we may infer that the variable (x) has the value x.
Triangle Property
The product of diagonal components is indeed equivalent to the product of determinants if all of the determinant elements above or below the main diagonal are formed entirely of zeros.
Conclusion
The reflection property, the all-zero property, the proportionality or repetition property, the switching property, the multiple scalar property, the sum property, the invariance property, the factor property, the triangle property, and the cofactor matrix property are some of the essential properties of determinants.
Other properties include the switching property, the multiple scalar properties, the sum property, and the cofactor matrix property, among many more.
Determiners have previously been introduced to us along with their definitions and representations. We have also learned about some of the applications of determinants and their qualities and significant aspects.




